2023届普通高等学校招生全国统一考试冲刺预测·全国卷YX-E(二)2数学试卷 答案(更新中)

2023届普通高等学校招生全国统一考试冲刺预测·全国卷YX-E(二)2数学试卷 答案(更新中)，目前全国100所名校答案网已经汇总了2023届普通高等学校招生全国统一考试冲刺预测·全国卷YX-E(二)2数学试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

12.A由题意知AABD和BCD为等边三角形，取BD中点为E,连接AE,CE,则AE⊥BD,由平面ABD⊥平面CBD,平面ABD∩平面CBD=BD,故AE⊥平面CBD,AE=/ADDE=√62一3=35，易知球心O在平而BCD的投影为△BCD的外心O1·过E以DO作OH⊥AE于H,易得OH∥OE,OO∥HE,则在R1△OHA中，OH=3,AH=25,所以外接球半径R=OF+AH平=√5，连接OM,因为AH=2HE,OH∥CE,AM=2MC,所以，H,O,M三点共线，所以OAM一MH一OH一√，当M为截面圆圆心时截面面积最小，此时载面圆半径r-(15)2-(/3)2=25,面积为12.故选A

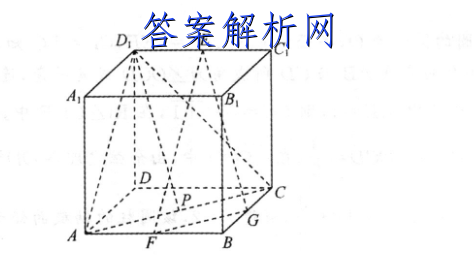
9.已知正方体ABCD-A1B1C1D1的棱长为2，E,F,G分别是棱D1C1,AB,BC的中点，P是底面ABCD内（包括边界)的动点，PD1∥平面EFG,则PD1的最小值为A.2B.√5C.√6D.22【答案】C【解析】知图，连接AC,AD1,CD1,因为E,F,G分别是棱D,C1,AB,BC的中点，所以AF=2AB,D1E=D,C,FG∥AC.因为AB=D,C1,AB∥D,C,所以AF=D,E,AF∥D1E,所以四边形AFED,为平行形，所以EF∥AD1.因为AD,丈平面EFG,EFC平面EFG,AC丈平面EFG,FGC平面EFG,所以AD1∥平面EFG,AC∥平面EFG,又AC∩AD1=A,所以平面ACD1∥平面EFG,所以点P在AC上移动时，PD1∥平面EFG,所以当AC⊥PD1时，PD1取得最小值.因为△ACD1为等边三角形，所以当P为AC的中点时，AC⊥1.因为正方体ABCD-A:B1C,D,的棱长为2，所以AC=AD,=CD,=22,所以PD,=X2E=6,所PD1的最小值为√6.DECABGAB