非凡吉创2022-2023高三届级TOP二十名校调研模拟卷三文数答案试卷 答案(更新中)

非凡吉创2022-2023高三届级TOP二十名校调研模拟卷三文数答案试卷 答案(更新中)，目前全国100所名校答案网已经汇总了非凡吉创2022-2023高三届级TOP二十名校调研模拟卷三文数答案试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

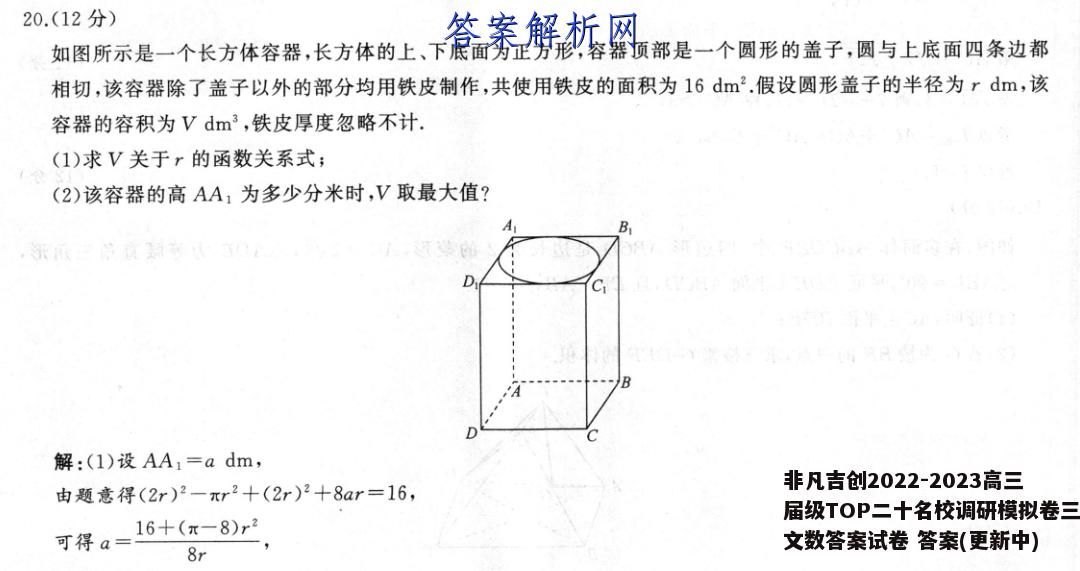
20.(12分)如图所示是一个长方体容器，长方体的上、下底面为正方形，容器顶部是一个圆形的盖子，圆与上底面四条边都相切，该容器除了盖子以外的部分均用铁皮制作，共使用铁皮的面积为l6dm2.假设圆形盖子的半径为rdm,该容器的容积为Vdm3,铁皮厚度忽略不计.(1)求V关于r的函数关系式；(2)该容器的高AA1为多少分米时，V取最大值？装解：(1)设AA1=adm,由题意得(2r)2-πr2+(2r)2+8ar=16,可得a=16+(π-8)r28r所以V=(2r)2a=8r+(2-4r(3分)由a>0,得16+（-8r>0,解得0<<8r8-π(5分)所以v=8r+(臣-4，r(08元)(6分)(2)由1D得V=8+3(2-42,(7分)令V>0,得0r<38=元4用通()来，预大识A6出44所以当r=√3(8-π)时，V取最大值，此时a=38-3(11分)即该容器的高AA,为382dm时，V取最大值.3(12分)

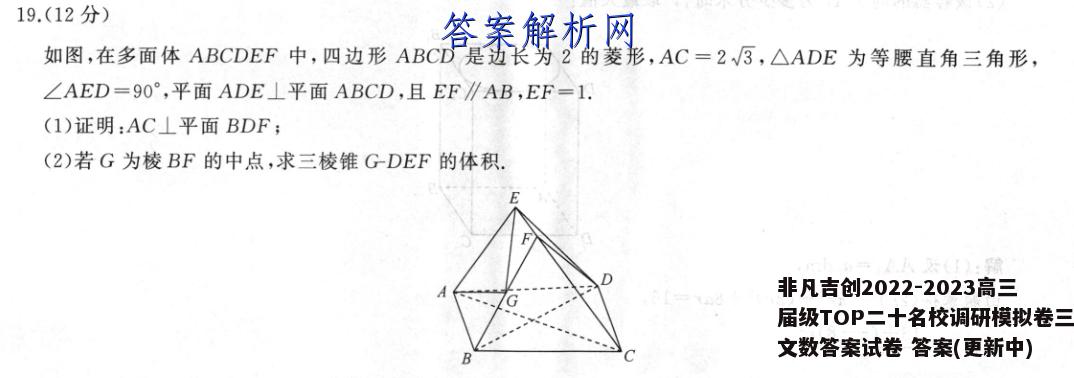
19.(12分)如图，在多面体ABCDEF中，四边形ABCD是边长为2的菱形，AC=2√3，△ADE为等腰直角三角形，∠AED=90°，平面ADE⊥平面ABCD,且EF∥AB,EF=1.(1)证明：AC⊥平面BDF;(2)若G为棱BF的中点，求三棱锥GDEF的体积.=人太(I):霸8“）一0卧国(1)证明：如图，取AD的中点H,连接EH,中5A余就余时心O融因为△ADE为等腰直角三角形，∠AED=90°，所以EH⊥AD,因为平面ADE⊥平面ABCD,且平面ADE∩平面ABCD=AD,所以EH⊥平面ABCD.(2分)设AC,BD的交点为0，连接OF.0H,则OH∥AB,且0H=AB=1,因为EF∥AB,EF=1,所以EF∥HO,且EF=HO,所以四边形EFOH为平行四边形，故FO∥EH,且FO=EH,所以FO⊥平面ABCD,所以FO⊥AC.(4分)在菱形ABCD中，有AC⊥BD,因为FO∩BD=O,FO,BDC平面BDF,所以AC⊥平面BDF.(6分)(2)解：因为AB=BC=2,AC=2√3，所以BO=1,BD=2,又△ADE为等腰直角三角形，∠AED=90°，AD=2,是MA所以EH=1,FO=1,给点因又EH∥FO,FOC平面BDF,EH史平面BDF,所以EH∥平面BDF,又G为棱BF的中点，所以V三技：GDEF=12(12分)