炎德英才·名校联考联合体2023届春季高二第一次联考(3月)政治答案试卷 答案(更新中)

炎德英才·名校联考联合体2023届春季高二第一次联考(3月)政治答案试卷 答案(更新中)，目前全国100所名校答案网已经汇总了炎德英才·名校联考联合体2023届春季高二第一次联考(3月)政治答案试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

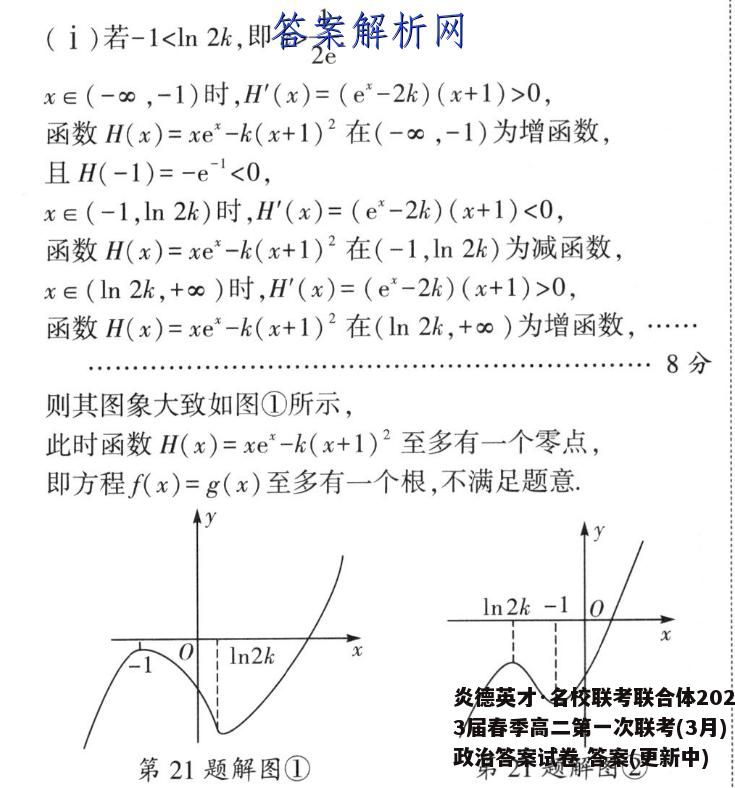
21.解：(1)f(x)=xe,所以f'(x)=e*(x+1),g(x)=k(x+1)2,所以g'(x)=2k(x+1),…2分故函数g(x)=k(x+1)2的图象在x=-1处的切线斜率为g'(-1)=0,所以f'(x0)=e0(xo+1)=0.解得xo=-1,则f(o)=f代-1)=-故对应切点坐标为(-1，).…4分(2)方程f(x)=g(x)可化为f(x)-g(x)=0,即xe*-k(x+1)2=0记H(x)=xe-k(x+1)2,则H'(x)=（e-2k)(x+1),方程f(x)=g(x)在区间(-∞，-1)，（-1，+∞)各恰有一个根m,n,且满足m+n<-2,可转化为函数H(x)=xe-k(x+1)2在区间(-∞，-1)，(-1,+∞）各恰有一个零点m,n,且满足m+n<-2,…6分(a)当k>0时，由H'(x)=(e-2k)(x+1)=0,得x1=-1,x2=ln2k.(i)若-1 2e(i)若-1 2ex∈(-∞，-1)时，H'(x)=(e-2k)(x+1)>0,函数H(x)=xe-k(x+1)2在(-0，-1)为增函数，且H(-1)=-e<0,xe(-1,ln2k)时，H'(x)=(e-2k)(x+1)<0,函数H(x)=xe*-k(x+1)2在(-1，ln2k)为减函数，x∈(ln2k,+∞)时，H'(x)=(e-2k)(x+1)>0,函数H(x)=xe-k(x+1)2在(ln2k,+o)为增函数，…8分则其图象大致如图①所示此时函数H(x)=xe-k(x+1)2至多有一个零点，即方程f(x)=g(x)至多有一个根，不满足题意In2k -1X第21题解图①第21题解图②(i)若1n2k<-1,即0 0,函数H(x)=xe-k(x+1)2在(-o,ln2k)为增函数，x∈(ln2k,-1)时，H'(x)=(e-2k)(x+1)<0,函数H(x)=xe-k(x+1)2在(ln2k,-1)为减函数，且H(ln2k)=ln2k·en2-k(ln2k+1)2=2kln2k-k(1n2k+1)2=-k(ln22k+1)<0,x∈(-1，+0)时，H'(x)=(e-2k)(x+1)>0,函数H(x)=xe*-k(x+1)2在(-1，+∞)为增函数，1且H(1)=e-46>e-4x2元>0其图象大致如图②所示，此时函数H(x)=xe*-k(x+1)2至多有一个零点，即方程f(x)=g(x)至多有一个根，不满足题意.…10分(b)当k<0时，令H'(x)=(e-2k)(x+1)>0,解得x>-1,令H'(x)=(e-2k)(x+1)<0,解得x<-1,所以函数的单调递减区间是(-∞，-1)，单调递增区间是(-1，+∞)，且-1)=-1<0，e因为m,n为方程f(x)=g(x)的两个根，则m,n必定一个大于-1，一个小于-1，不妨设m<-1,n>-1,要满足m+n<-2,只需满足m<-2-n<-1,因为H(x)在(-∞，-1)单调递减，所以只需满足H(m)>H(-2-n),又H(m)=H(n)=0,即需满足H(n)>H(-2-n),令G(x)=H(x)-H(-2-x）,x∈(-1，+0)，则G(x)=xe-k(x+1)2-(-2-x)e2-+k(-2-x+1)2=xe+(2+x)e2-x,则G'(x)=(+1)(e-e2=（+(ea-1.因为x∈(-1，+∞)，所以G'(x)>0,即G(x)在(-1，+∞)上单调递增所以G(x)>G(-1)=0,即H(n)>H(-2-n),故满足m+n<-2,综上，若方程f(x)=g(x)在区间(-∞，-1)，(-1，+∞)各恰有一个根m,n,且满足m+n<-2,则k的取值范围为(-∞，0).12分

7.B【考查点】本题考查平面向量的夹角【解析】解法□因为(a-b)⊥b,所以(a-b)·b=a·b-b2=0,即a·b=b2,又因为|al=2Ib|,所以cos(a,b)=a:b1之a·b1又向量夹角为[0，T],故a与b的夹角为3第7题解图解法二因为非零向量a,b满足(a-b)⊥b,如图：[点拨]根据（α-b)⊥b,联想到利用圆的切线与半径垂直来作图.又1a=21b1,由图可知a与b的夹角为”