2022~2023学年核心突破QG(二十)20生物试卷 答案(更新中)

2022~2023学年核心突破QG(二十)20生物试卷 答案(更新中)，目前全国100所名校答案网已经汇总了2022~2023学年核心突破QG(二十)20生物试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

10.A【考查点】本题考查三角函数的图象与性质【解析】由x)=cosx-sinx=2cos(x+牙），[易错]容易混淆余弦两角和、差公式而致错得f代)的单调递减区间为2km≤x+4≤2km+m(k∈Z),T解得26n4≤≤2m+（keZ，得x)在[2km牙，2hm+31(keZ)单调递减，取=0，得)的一个减区间为[-年，31。又f(x)在[-a,a]单调递减，则0

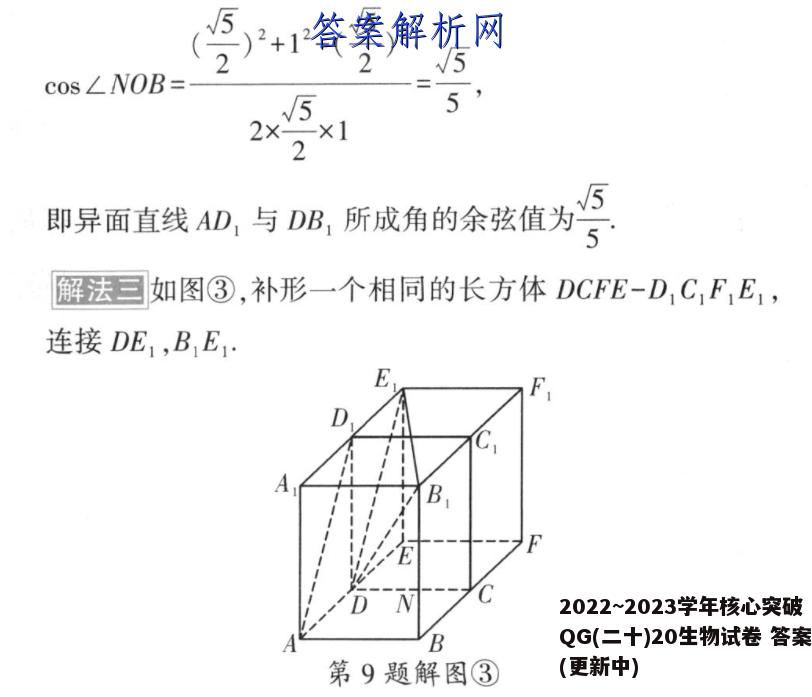
9.C【考查点】本题考查异面直线所成角，【解析】解法一在长方体中以A为坐标原点，分别以AB,AD,AA所在直线为x轴，y轴，z轴建立空间直角坐标系A-xyz,如图①所示，AB=BC=1,AA1=√3，则A(0,0,0),D(0,1,3),D(0,1,0),B(1,0,3),B则AD,=(0,1,3),DB=(1,-1,N3),设异面直线AD,与DB,所成角为0，则cos0=AD:DB:5第9题解图①IAD IDBI[易错]容易忽略异面直线所成角的范围(0，)]而致错，5即异面直线AD,与DB,所成角的余弦值为解法□如图②，连接BC,与B,C交于点O,取CD中点N,连接ON,NB.则ON∥DB1,AD1BC1DBA第9题解图②则ON与OB所成角∠NOB即为异面直线AD,与DB,所成角.[点拨]通过平行关系将异面直线转化为相交直线，从而得到异面直线所成角.在长方体中，B,D=1+1+3=√5，ON2OB2BC,-BGCC-1,故在△NOB中，由余弦定理得+1-()、cos∠NOB=√552×2×12√5即异面直线AD,与DB,所成角的余弦值为5解法三如图③，补形一个相同的长方体DCFE-D,C,F,E,,连接DE1,BE1AB第9题解图③易知AD1∥DE,则∠B,DE,为异面直线AD,与DB,所成角因为在长方体ABCD-A,B,C,D1中，AB=BC=1,AA1=√3，所以DE,=W/12+(3)2=2,DB,=W/12+12+(5)2=√5，B,E1=√12+22=√5，在△B,DE,中，由余弦定理，得cos∠B,DE,=2+(5)2-(5)2√52x2x/551√5即异面直线AD,与DB,所成角的余弦值为