安徽2023届江南十校一模英语试卷 答案(更新中)

安徽2023届江南十校一模英语试卷 答案(更新中)，目前全国100所名校答案网已经汇总了安徽2023届江南十校一模英语试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

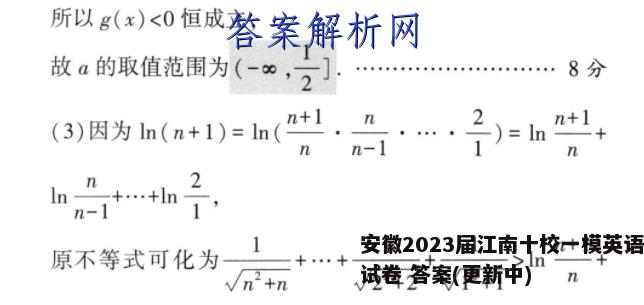
22.【解析】审题指导a=1导函数(1)fx)(x)f(x)单调性求导正负(2/x)<-1>0fx+1<0恒成立利用单调a的范围性求最值构造函数g(x(3)要证不等式→利用对数性质，化简不等式利用函数单调利用换元将其转性判断并证明化并构造函数解：(1)当a=1时，f(x)=xe-e,f'(x)=xe,…2分当x>0时，f'(x)>0,f(x)单调递增；当x<0时，f'(x)<0,f(x)单调递减。…4分(2)当x>0时f(x)<-1,令g(x)=f八x)+1=xe-e*+1,即g(x)<0在(0，+∞)上恒成立，g'(x)=e(1+ax)-e,g'(0)=0,g"(x）=ae“(2+ax）-e,g"(0)=2a-1,…6分当2-10，即a时g)>0g)单调道增。又g'(0)=0,所以g'(x)>0,g(x)>g(0)=0,与g(x)<0恒成立矛盾：当2a-1≤0，即a≤)时，g(x)≤0，g(x)单调递减，又g'(0)=0,所以g'(x)<0,g(x) 1),即证2lnx

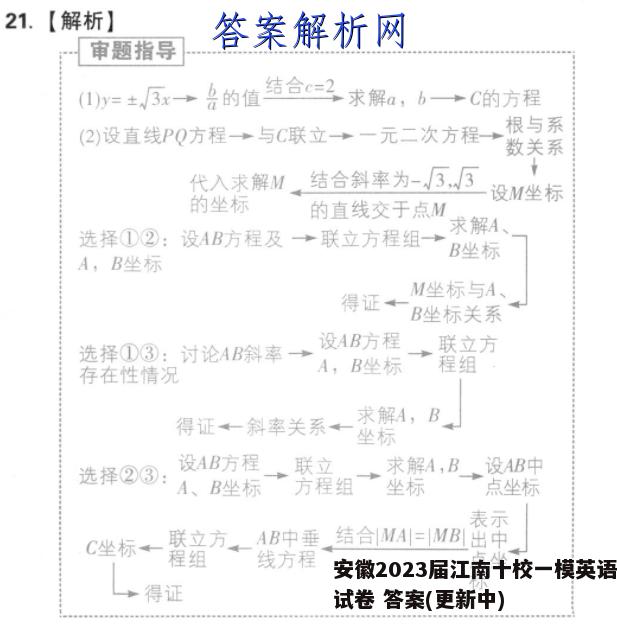
21.【解析】审题指导(1)y=±3x→的值结合c=2求解a,b→C的方程(2)设直线PQ方程→与C联立→一元二次方程→根与系数关系代入求解M结合斜率为-3,3的坐标设M坐标的直线交于点M求解A选择①②：设AB方程及→联立方程组→B坐标A,B坐标M坐标与A、得证B坐标关系选择①③：讨论AB斜率设AB方程联立方存在性情况A,B坐标程组得证←斜率关系←求解A,B坐标设AB方程选择②③：联立求解A,B设AB中A、B坐标方程组坐标点坐标表示C坐标联立方AB中垂结合MA=MB出中程组线方程点坐得证解：(1)由题意可得6=3，√公+6=2，解得a=1,b=√3，因此C的方程为-号=1…4分(2)设直线PQ的方程为y=kx+b(k≠0)，将直线PQ的方程代入2-号=1可得(3-2)x2-2x-62-3=0,32kb62+3所以+3-，=3-k2所以名=√+)4批，-25·+3-3-k2…5分au生g两式相减可得y,-y2=23xw-√3(x,-x2),因为y1-y2=k(x1-x2),所以23xM=√3(x,+x2)+k(x1-x2）,解得wk√6+3-k+kb…7分3-k2两式相加可得2yM-(y,+y2)=√3(x,+x2),又y1+y2=k(x1+x2)+2b,所以2yw=√3(x1-x2）+k(x1+x2)+2b,解得w=3V+3-+363-k2所以w=xw,其中为直线P0的斜率；…9分选择①②：设直线AB的方程为y=k(x-2),A(x3,y3),B(x4,y4),=k(x-2)则,解得x,2k23k,=5k-√3k-√3同理可得x4=2k23k11分+√3k+√/34k212k所以+-3+y-3(yw=k(xw-2)2K2此时点M的坐标满足3,解得xM=k2-3所以M为AB的中点，即IMA|=IMBI.12分选择①③：当直线AB的斜率不存在时，点M即为点F(2,0),此时不在直线y=上，矛盾。3当直线AB的斜率存在时，设直线AB的方程为y=m(x-2)(m≠0)，设A(x3,y3),B(x4,y4）,y3=m(x3-2)2m23m则,解得x3y3=3x3k-√3k-√32m23m同理可得x4=y4=11分m+√3m+√3此时w)所以6m2-3由于点同时在直线y=}上，者6m=-·2m2,解得k=m,因此PQ∥AB.12分选择②③：设直线AB的方程为y=k(x-2),设A(x3,y3),B(x4,y4),则y=k(x3-2)y,=3x2k23k解得x3k-√3,Y3=k-√52k23k同理可得x4=11分k+3k-√3设相的中点Ce).则c=西+)-==6k-3由于IMAI=IMBI,故M在AB的垂直平分线上，即点M在直线ye=(x)上，将该直线与y=联立，32k6k解得xmk2-=xc.YM=R-3=yc,即点M恰为AB中点，故点M在直线AB上.…12分