天一大联考 2022-2023学年高中毕业班阶段性测试(五)5英语试卷 答案(更新中)

天一大联考 2022-2023学年高中毕业班阶段性测试(五)5英语试卷 答案(更新中)，目前全国100所名校答案网已经汇总了天一大联考 2022-2023学年高中毕业班阶段性测试(五)5英语试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

20.【解析】审题指导设F为(1)要证OE∥平面PACAE中点需证平面OEF∥平面PACE为PB中点EF∥PA→EF∥平面PACOF∥平面PACF为AB中点PF⊥ABAB⊥PA=PBPO⊥AB-平面POF6士-0cPO为三棱锥→PO⊥平面ABCP-ABC的高(2)结合(1)中垂∠ABO=∠CB0=30°相应线相应点直关系建系P0=3.PA=5段长坐标二面角平面CAE.ABEC-AE-B-A元AA店的余弦值的法向量同角三角二面角C-AE-B的正弦值函数关系解：(1)如图，取AB中点F,连接OF,PF,EF,又E为PB的中点，所以EF∥PA,因为EFt平面PAC,PAC平面PAC,所以EF平面PAC.1分因为PA=PB,F为AB中点，所以PF⊥AB,又P0是三棱锥P-ABC的高，所以PO⊥AB,又PO∩PF=P,PO,PFC平面POF,所以AB⊥平面POF,第20题解图因为OFC平面POF,所以AB⊥OF.3分因为AB⊥AC,所以OF∥AC因为OF￠平面PAC,ACC平面PAC,所以OF∥平面PAC,5分因为OF∩EF=F,OF,EFC平面OEF,所以平面OEF平面PAC,又OEC平面OEF,所以OE平面PAC.…6分[点拨]由于无法直接利用线面平行的判定定理证明线面平行，故考虑利用面面平行的性质定理“若两平面平行，则其中一平面内的任意一条直线均与另一平面平行”进行求证(2)如图，连接OA,因为P0是三棱锥P-ABC的高，故PO⊥平面OAB,故分别以OF,OP为x,z轴，以过O且垂直于OF的直线为y轴建立空间直角坐标系.因为∠AB0=∠CB0=30°，P0=3,PA=5,F为AB中点且0F⊥AB,所以OA=0B=4,所以A(2,-2W3,0),B(2,2N3,0),P(0,0,3),E(1,5,T所以AB=4W3.因为AB⊥AC,∠ABC=∠ABO+∠CBO=3则AC=12,所以C(-10,-23,0),则花=(-120,0)，A店=(-1,33，)，店=(0,4w3,0),…8分设平面CAE的法向量为m=(x1,y1,,),m·AC=0-12x1=0可得即3-x+35+2=0则=0，取=2，则=所以m=(0,百2.设平面ABE的法向量为n=(x2,y2,22),n·AB=043y2=0=0+3%+=0可得则y2=0,取2=2，则x2=3,所以n=(3,0,2),…10分m·n443所以cos(m,n〉=Imlinl3133×3故二面角G-AB-B的正弦值为，1-(4W3、111312分

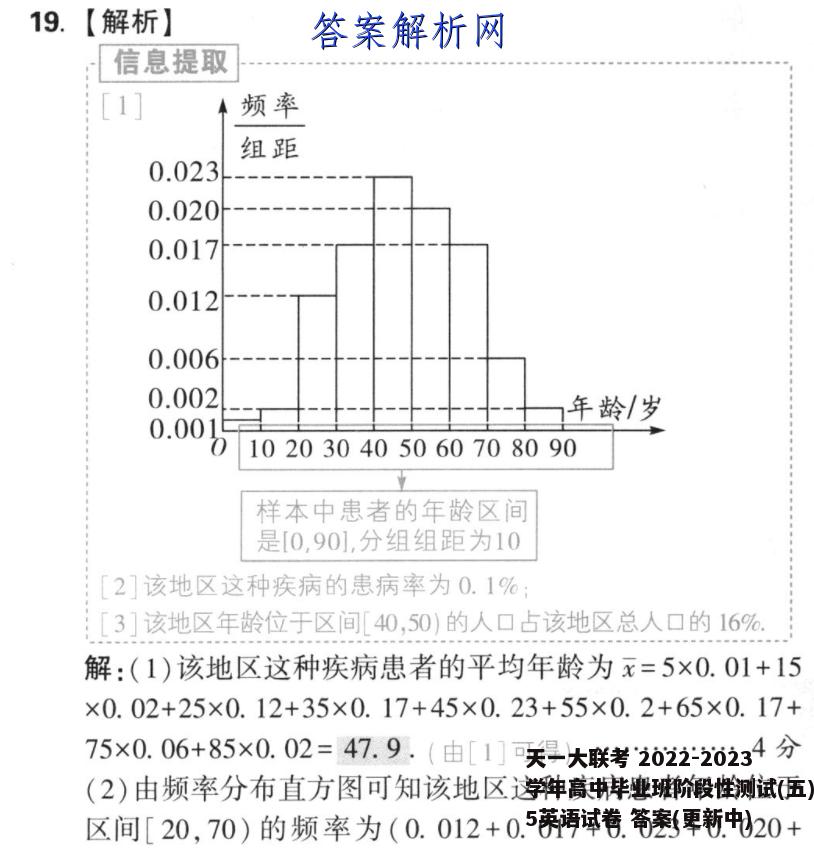
19.【解析】信息提取[1]频率组距0.0230.0200.0170.0120.0060.002年龄/岁0.001102030405060708090样本中患者的年龄区间是[0,901，分组组距为102]该地区这种疾病的患病率为0.1%:[3]该地区年龄位于区间[40,50)的人口占该地区总人口的16%，解：(1)该地区这种疾病患者的平均年龄为x=5×0.01+15×0.02+25×0.12+35×0.17+45×0.23+55×0.2+65×0.17+75×0.06+85×0.02=47.9.(由[1]可得)…4分(2)由频率分布直方图可知该地区这种疾病患者年龄位于区间[20,70)的频率为(0.012+0.017+0.023+0.020+0.017)×10=0.89,(由[1]可得6分频率估计概率可知该地区一位这种疾病患者的年龄位于区间[20,70)的概率为0.898分(3)用A,B分别表示此人患病、此人年龄位于区间[40,50)的事件9分P(AB)则P(A)=0.1%,P(B)=16%,P(A1B)=P(B)0.1%×0.23≈0.0014.（由[2]，[3]可得】11分16%故此人年龄位于区间[40,50)时患这种病的概率为0.0014.12分