2023届衡中同卷 信息卷 全国卷A 文数(一)1试题答案

2023届衡中同卷 信息卷 全国卷A 文数(一)1试题答案，目前全国100所名校答案网已经汇总了2023届衡中同卷 信息卷 全国卷A 文数(一)1试题答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

3317.解：(1)因为/3sinC-cosC=二b,所以wW3sinC-cosC-如C-sinBsin A整理得/3 sin Csin A-cos Csin A=sinC-sinB,……2分又B=x-(A+C),所以sinB=sin(A+C)=sin Acos C+cos Asin C,所以W3 sin Csin A+cos Asin C-=sinC,因为C∈(0，π)，所以sinC≠0，所以W/5sinA+osA=1,即sm(A+晋)=2，4分因为A∈(0，x),所以A+音∈（晋，看），所以A+吾=即A受6分(2)因为AD为△ABC的角平分线，所以∠BAD-∠CAD=于，1，D,00800所以Sx=SAm+Sa-之c·ADn号+2b:ADsn吾，即25-号(c+b),商平所以b+c=6.8分又Sac=2csn等=坠-23，所以x=8,49分由余弦定理得a2=+e-2bc0s写=(b十c)2-c=28,所以a=2/7,11分所以△ABC的周长a十b十c=6十2√7.…12分

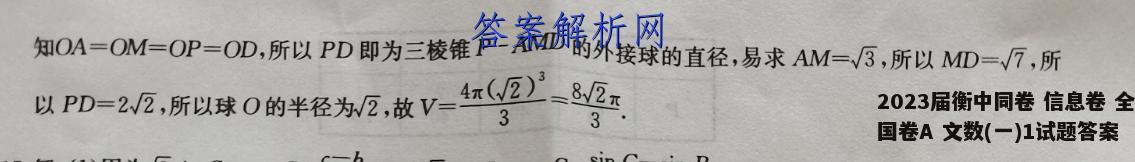
16.8√2π由题意知AM⊥BC,故AM⊥PM,当平面PAM⊥平面AMCD时，三棱锥P-AMD的体积最大.此时平面PAM⊥平面AMCD,平面PAM∩平面AMCD=AM,AM⊥PM,PMC平面PAM,所以PM⊥平面AMCD,又DMC平面AMCD,故PM⊥DM因为MC∥AD,AM⊥MC,所以AM⊥AD,易证PM⊥AD,又PA∩PM=P,PA,PMC平面BPAM,所以AD⊥平面PAM,故AD⊥PA,取PD的中点O,连接OA,OM,由直角三角形斜边上的中线性质知OA=OM=OP=OD,所以PD即为三棱锥P-AMD的外接球的直径，易求AM=3,所以MD=√7，所以PD=22,所以球0的半径为反，放V-红)-833