长郡、雅礼、一中、附中联合编审名校卷2023届高三月考试卷五5(全国卷)物理/答案

长郡、雅礼、一中、附中联合编审名校卷2023届高三月考试卷五5(全国卷)物理/答案，目前全国100所名校答案网已经汇总了长郡、雅礼、一中、附中联合编审名校卷2023届高三月考试卷五5(全国卷)物理/答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

21.【解析】(1)抛物线C的焦点为F(0,1),即c=1,椭圆上的点M到点F的最大距离为a+c=3,所以a=2,b2=3,所以椭圆方程为上+父=143(2)抛物线C的方程为=4，即y=千，对该函数求导得y-于4设点A(x,片)，B(22),M(),直线M1的方程为y-y=之(x-),即y=号-y,即x-2%-2y=0同理可知，直线MB的方程为x2x-2y2-2y=0,由于点M为这两条直线的公共点，则x1x0-2y-2y=0x2七-2y2-2=0所以点A,B的坐标满足方程xx-2y-2y=0,所以直线AB的方程为xx-2y-2y=0,xx-2y-2y%=0联立,可得x2-2xx+4=0,由韦达定理可得x+x2=2x，xx2=4y%,新以h--月*-4--96c-16-G+4G-点M到直线AB的距离为dx-4Vx6+4所烈5国d--4切-代-，253由已知可得-2”y”2,所以当y=-2时，△MAB面积的最大值为8√2.

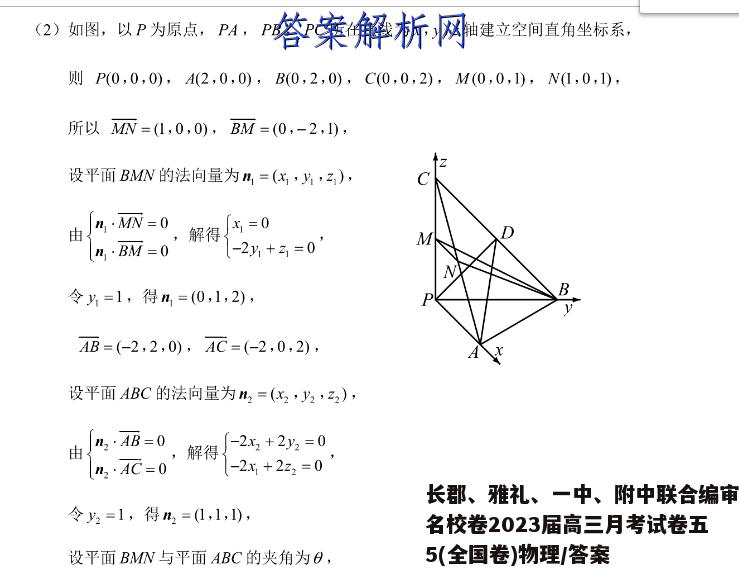
(1)因为M,N分别为PC,CA的中点，所以MN∥PA:因为BM⊥MN,所以PA⊥BM,取BC中点为D,连接PD,AD,因为P-ABC为正三棱锥，所以BC⊥PD,BC⊥AD,且PD∩AD=D,所以BC⊥平面PAD,所以BC⊥PA,又BM∩MN=M,所以PA⊥平面PBC;所以mP=2x2-4设点P到平面ABC的距离为d,所以cd=254,因为c=y,c,所以d=2所以点P到平面ABC的距离为3(2)如图，以P为原点，PA,PB,PC所在直线为x,y,z轴建立空间直角坐标系，则P(0,0,0),A(2,0,0),B(0,2,0),C(0,0,2),M(0,0,1),N(1,0,1),所以MN=(1,0,0),BM=(0,-2,1),设平面BMN的法向量为m=(:,片，z),Cn,·M不=0由，解得=0n·BM=0-2y+名=0'MD令片=1，得h=(0,1,2),BAB=(-2,2,0),AC=(-2,0,2),设平面ABC的法向量为n2=(x2,2,22),n2·AB=由0,解得-2.x2+2y2=0n2·AC=-2x+2z2=0令2=1，得2=(1,1,1)，设平面BMN与平面ABC的夹角为B,所以cos0=1%·n_V15|ln2|5所以平面BMN与平面ABC夹角为余弦值为√5