2023普通高等学校招生全国统一考试新高考仿真卷(二)2物理试卷 答案(更新中)

2023普通高等学校招生全国统一考试新高考仿真卷(二)2物理试卷 答案(更新中)，目前全国100所名校答案网已经汇总了2023普通高等学校招生全国统一考试新高考仿真卷(二)2物理试卷 答案(更新中)的各科答案和试卷，更多全国100所名校答案请关注本网站。

22.（12分)【解答】(1)令h(x)=f(x)+g(x)=tanx+sinx-2x,则)+cosx-2-1-cos)(1+cosx-cos)cos2x当xe0到时，0 0,1+cos-cos2x0,从而公(>0.因此，A()在0哥)内单调道增。当x0时，Ax>hAo=-0,即f)+8()>0.(2)解法一：令p(x)=f(x)+g(2x)=tanx-2x+asin2x,则由题意，任1-受+a20,即a≥号-1.（必要条作）若≥号1，则当xe0引时，由m220,有m-2(-小2x下面证明：当x[0引时，amx-2x+任-小如2x之0.…0令p=m-2r+侣-小n2x,x0引则pjFo24(r-2l水as2x-2os-[-21eo3-lcos-x◆pe-0,用m号喷s”停小即=导政=a,脚a0别且cmu点由y=ows在0内单调递减且恒大于0，可得p(x)的单调性如下：(0.a)aa,44-2p'(x)+00+p(x)单增极大值单减极小值单增国为n0=0且)-0.所以当xe0引时，p(x)20,即①式成立.由此.若a≥号-1，则当xe[0引时，（上p叫20，符合题意，（充分条件综上所述，实数0的取值范围为[行一山+网解法二：首先证明不等式：当xe0引时，m-x>0.p-m,当到味p0,pa内单增，由此，当xe0)时，p()>p0)=0,即amx-x>0,不等式得证.下面回到原题.当x=0时，不等式显然成立当0时，由sin2x>0,原不等式可化为。12x2cos2x sin2x+a20.令pl-20xs2+a,则p-4-mcs2x.令p)=0,得x=sin2 2x当x0引时，m2x>0,0,从面在0内单调递减：当xe(任引时，2<0.p>0,从p在（年引内单调递增.所以，()在0内存在最小值且o=(目}-1-号+a由愿意，似之0，即a≥号-1.综上，实数a的取值范调为对[侣-+D由图象可知，-5≤≤0，即-5≤a50.22所以，实数a的取值范围为[-V5,0]·由图象可知，1+6=π，5-4=2π，即4(x+x)-2=π，4(5-)=2m·(i)5π所以，+=125π=-π,x-为=-7，从而2x1+x2-x=122=m2+=m（=sinππππcosπnπV2-√6=sin-cos--cos-sin-4343X34

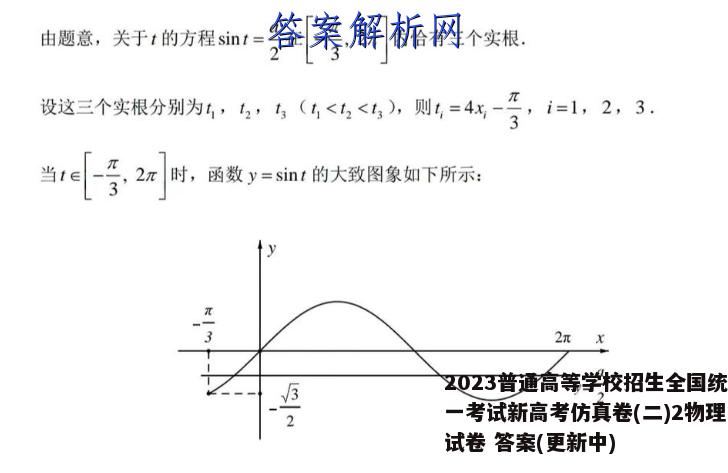
21.(12分)【解卷1wrw=2n(-}m个-引2ow(-}-=m2x-}5em个2x-2）-2sm2x-引令2a-号≤2x-号≤2x+号keZ,解得k红≤xSk+π12keZ.2所以国的单调造指区同为[红-受：+，keZ。2》86=f2)-a=2n4r-}a4=4-营则当x0时，[景2]由题盒，关于1的方程1=号在[号2内恰有三个实根，2由题意，关于1的方程：号在[子2]内恰有三个实根.设这三个实根分别为4,4，与（4<5<%，则=4钙-写i=1,2,3.当[管2时，西数y=:的大致图象如下所示：π2πxay=2