2023年普通高等学校招生全国统一考试 23·JJ·FZMJ 金卷仿真密卷(二)2物理答案

2023年普通高等学校招生全国统一考试 23·JJ·FZMJ 金卷仿真密卷(二)2物理答案，目前全国100所名校答案网已经汇总了2023年普通高等学校招生全国统一考试 23·JJ·FZMJ 金卷仿真密卷(二)2物理答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

22.【命题意图】本题考查参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化、点到直线的距离公式，体现了数学运算、直观想象、逻辑推理等核心素养[x=√3sin0-cos0+2,【解】(1)曲线C:(0为参数)，Ly=sin 0+/3cos 0消去0并整理，得(x-2)2+y2=4,即曲线C,的普通方程为(x-2)2+y2=4(2分)由2psin0-4)-4=0得psin0-pcos0-4=0,因为x=pcos0,y=psin8,所以y-x-4=0.故直线l的直角坐标方程为x-y+4=0.(5分)】(2)方法一设P(2+2cosa,2sina),则点P到直线1的距离d=2cosa-2sina+612-22ma-+6(8分)√2当ma)=-1时，点P到直线1的距离取得最大值，且d.m=2+32;当mQ-)=1时，点P到直线1的距离取得最小值，且d=-2+3√2.(10分)方法二由(1)知曲线C,的轨迹是以(2,0)为圆心，2为半径的圆所以圆心(2,0)到直线1的距离d=12-0+41=32.2(8分)】因为点P在曲线C1上，所以点P到直线的距离的最大值为32+2，最小值为32-2.(10分)

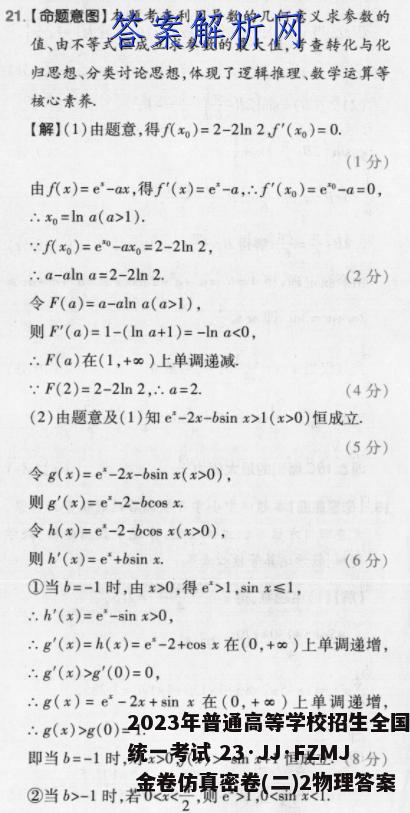
21.【命题意图】本题考查利用导数的几何意义求参数的值、由不等式恒成立求参数的最大值，考查转化与化归思想、分类讨论思想，体现了逻辑推理、数学运算等核心素养【解】(1)由题意，得f代xo)=2-2ln2f'(xo)=0.(1分)】由f八x）=e'-ax,得f'(x)=e-a,∴f'(xo）=e"-a=0,∴.xo=lna(a>1).f（xo)=eo-axo=2-2n2,,∴.a-alna=2-2ln2.(2分)】令F(a)=a-alna(a>l),则F'(a)=1-(na+1)=-lna<0,∴.F(a)在(1，+e)上单调递减..F(2)=2-2n2,∴.a=2.(4分)】(2)由题意及(1)知e-2x-bsin x>1(x>0)恒成立(5分)g(x)=e*-2x-bsin x(x>0),则g'(x)=e-2-bcos x.4h(x)=e"-2-bcos x(x>0),则h'(x)=e+bsin x.(6分)①当b=-1时，由x>0,得e>1,sinx≤1，∴.h'(x)=e'-sinx>0,∴g'(x)=h(x)=e-2+cosx在(0，+o)上单调递增，∴.g'(x)>g'(0)=0,∴g(x)=e-2x+sinx在(0，+o)上单调递增，.g(x)>g(0)=1.即当b=-1时，对x>0,f代x)>-sinx+1恒成立.(8分)】②当b>-1时，若0 1,0 0时，h'(x)=e+bsin x>0.当b=0时，h'(x)=e>0.当-1 0.“当xe0,)时，h'(x)>0,即g'(x)=h(x)=e-2-beos在0,2)上单调递增g(0)=-1-b<0,82）=e3-2>0,3e0,),使得g()=0,且当xe(0,)时，g'(x)<0,∴.g(x)=e-2x-bsin x在(0，x,)上单调递减，∴.当xe(0,x1)时，g(x)